Maths, Meet Stats

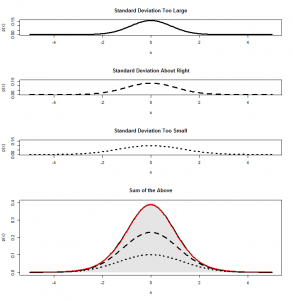
You might find this article interesting if you’re curious how the chi-Squared tests (such as goodness-of-fit) really work, but don’t feel you have the mathematical background to tackle the linear algebra that is involved with proving how they work. Instead of mathematical derivations, I’ll try to explain the tests through graphs and diagrams, so that you can gain some intuitions about what is going on inside the chi-squared tests. If you feel comfortable with more advanced mathematical concepts such as vectors and matrices (linear algebra) you might find my other post here more succinct/precise.

One of the reasons I wrote this was a realisation that there isn’t (as far as I could find) another post out there that really conveys the workings of the test (correctly) without fairly complicated maths. There are a few sites out there that try to simplify it, but they get it quite far wrong (by the end of this, I hope you’ll have the intuitions to see that they are indeed wrong). And wrong intuitions lead to people using the test in ways that simply don’t work, and I have seen this in my job many, many times.

To develop these intuitions, I’ll also need to introduce the chi-squared distribution. You might think this distribution is only really useful for chi-squared tests, but actually, the chi-squared distribution underlies almost every single parametric test that you will meet in an introductory stats course (t-tests, ANOVA, linear regression, ANCOVA, polynomial regression, all derive their p-values by means of chi-squared distributions) and the intuitions we’ll develop here can be extended to allow you to understand how these tests really work, in a much cleaner, more obvious way. In turn that will give you a clear understanding of concepts such as degrees of freedom, and type-I sums of squares, and how all the first parametric tests you learn are effectively the same test, rebadged. I will write a post on this, when I get the chance. But, for today, chi-squared, and in particular, the goodness-of-fit test. (The test for association is just an extension to this, but is a good deal harder to visualise).

You might gather, looking at the rest of this blog, that I have a small fascination for the chi-squared test. I find it fascinating that this test is so outwardly simple, so simple that it is often the first hypothesis test that a student will be taught, but whose workings under-the-bonnet are far more complicated than they seem to appear. It leaves us with this enigmatic formula that doesn’t seem to make much sense unless we can interrogate it with some relatively complex maths (certainly beyond the scope of many users of statistics).

The Chi-Square Distribution

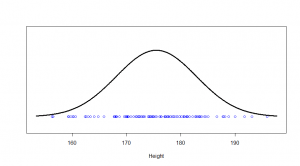
The one kind of distribution most people are familiar with is the normal distribution. Let’s start with that. Say, if I randomly picked 100 American men, their heights (in cm) might correspond to the dots on this:

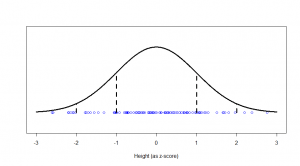
We see a big clump of people in the middle (the peak in our bell-curve indicates that we expect to find a lot of people of these heights) and fewer people as we head out to the tails. We might consider those people out in the tails as being “unusual” in the sense of their height, and in statistics, we’re often hunting for things that look “unusual”. The heights are normally distributed, but if we subtract the mean (175 cm) and divide by the standard deviation (7.4 cm), we get “z-scores”. Z-scores are distributed as what we would call a “standard normal” distribution (one with zero mean and standard deviation of one):

Now, this makes things much easier, because we know exactly what sort of z-scores are “usual”, and what sort of z-scores are more unusual. For example, 95% of all z-scores will lie between (around) -2 and +2. Those that are outside of those bounds, we very often consider “unusual”. Those between -1 and +1 are the most common.

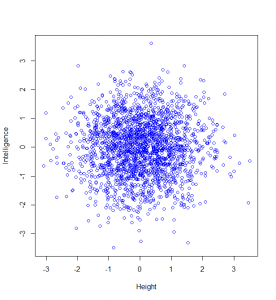
Now, let’s suppose we are going to measure people’s intelligence too. To keep this simple, I’m going to assume that intelligence and height are not correlated at all. Then a plot of 2000 people’s heights vs their respective intelligences (as z-scores), might look like this:

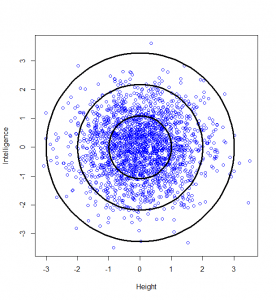
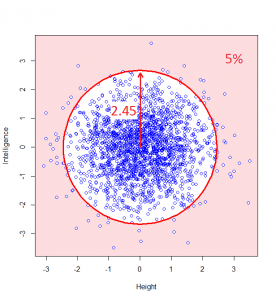
Now, maybe we want to find it if someone has a particularly unusual combination of intelligence and height? Someone who is extremely intelligent and extremely tall, for example. Well, this “bivariate” normal distribution seems to become sparser and sparser the further from the middle we are: in actual fact, one of the most wonderful properties of the normal distribution is that this happens in perfect circles (it might not sound that wonderful yet, but in later posts, we’ll see just how powerful this really is):

So, we can classify how normal someone is by their distance from the centre of this graph. For example, 95% of people will lie no more than a distance of 2.45 away from the middle:

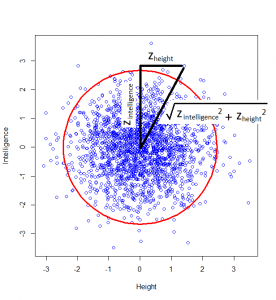
How do we calculate that distance? Good old Pythagoras theorem! If we square the height of a given person, square their intelligence score, and add those two squares, we get the square of the distance from the centre to their point on the graph.

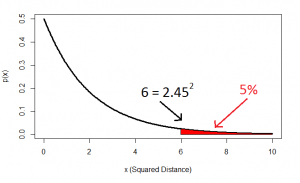
And this squared distance is the chi-square statistic. Obviously this was just the square of one standard-normal variable (height z-score) and another (intelligence z-score), and this gives us the idea of looking at the distribution of the sum of two squared normal variables: that distribution is the chi-square distribution with two degrees of freedom:

…and this confirms that, indeed, 5% of datapoints will lie at a squared distance greater than 6 (or an unsquared distance of 2.45).

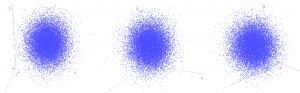
The same idea stretches to as many dimensions as you want. If we have three (uncorrelated) z-scores, they form spheres:

…and we can again calculate how “unusual” a particular combination of values is by finding the squared distance from the centre. This is calculated by an extension of Pythagoras (“Euclidean distance”), again by summing up the three squared individual values, and comparing to a chi-squared distribution with three degrees of freedom.

We can go on like this into as many dimensions as we want, the same always holds. And the degrees of freedom of the chi-squared distribution just represents the number of independent normal distributions we are combining.

The Chi-Squared Goodness-of-Fit Test

First things first, let’s make sure we have a definition of the goodness-of-fit test that is actually correct. The most common definition that I have seen is that it is a “test for count data”. While there is a kernel of truth to that, I have seen far too many instances where that has been misunderstood and the test has been wrongly used. I’ll explore some of those abuses in a later post, and we’ll see why they don’t work, at least without a few modifications to the test.

The goodness-of-fit test should instead be thought of as a proportion test. In a later post, I’ll describe how ANOVA generalises a t-test to test more than two means by replacing a normal distribution with a chi-squared distribution; the goodness-of-fit test generalises the proportion test to work on proportions of more than two categories in exactly the same way, as we’ll see. So, it’s a proportion test that can handle more than two categories.

Let’s start with an example where we are looking at the proportion of just two things, so that we can compare it with a proportion test. Say I’m going to toss a coin 100 times. How many heads will I get? On average, we might expect we’d get about fifty heads. This is our “expected” number of heads, which we’ll refer to with the letter “E”:

,

where is the number of times we toss our coin and is the probability of getting a head.

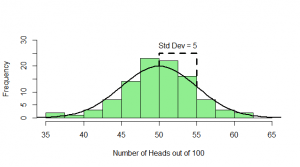
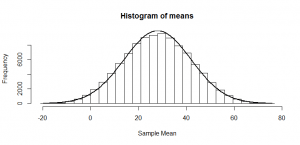
But, of course, we might not get exactly 50 heads. Let’s try repeating this experiment a hundred times and see how many heads we get each time:

Sometimes we get 55 heads, or 45. It’s not even that unusual that we get 60 or 40 heads. If we got 80 heads, we might start wondering if we really had a fair coin. By comparing our result to this histogram, we can figure out if our result looks like the sort of result we’d get from a fair coin (and, if not, we call our result “statistically significant” and reject our null hypothesis of a fair 50/50 coin).

Notice how much it looks like a normal distribution? This is actually a binomial distribution, but if we toss the coin enough times, it turns out to look (almost) exactly like a normal distribution, and we know from the properties of the binomial distribution what mean and standard deviation this normal-ish distribution will have:

,
,

which, in our case, is

,
.

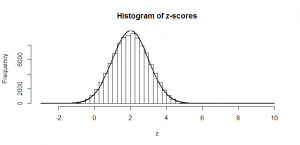
So, if we subtract the mean (50), and divide by the standard deviation (5), we can do just as we did at the start with our heights: subtract the mean, and divide by the standard deviation and the result is a -score that can be compared with the tables of standard normal values in the back of a book (since we now have mean zero and standard deviation of one). And this is precisely what the standard proportion test does:

,

where represents the number of heads we have “observed”.

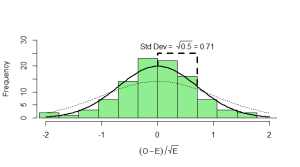
But the goodness-of-fit test takes a slightly more circuitous route to the answer. We’ll see why in a moment. After subtracting the mean (), instead of dividing by the standard deviation () we just divide by . Calculating , then we end up with something that has mean zero, but standard deviation of :

What can we do with this? We can’t compare it with our standard normal (which is dotted onto the graph for comparison). To see how this will work out, we need to consider both the number of heads and the number of tails:

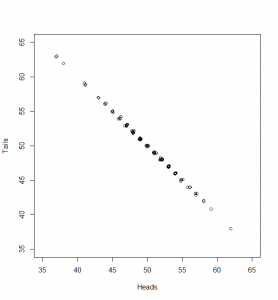
Now, if we subtract the expected number of heads from the heads and divide by as before, and the same (respectively) for tails, here’s what we get:

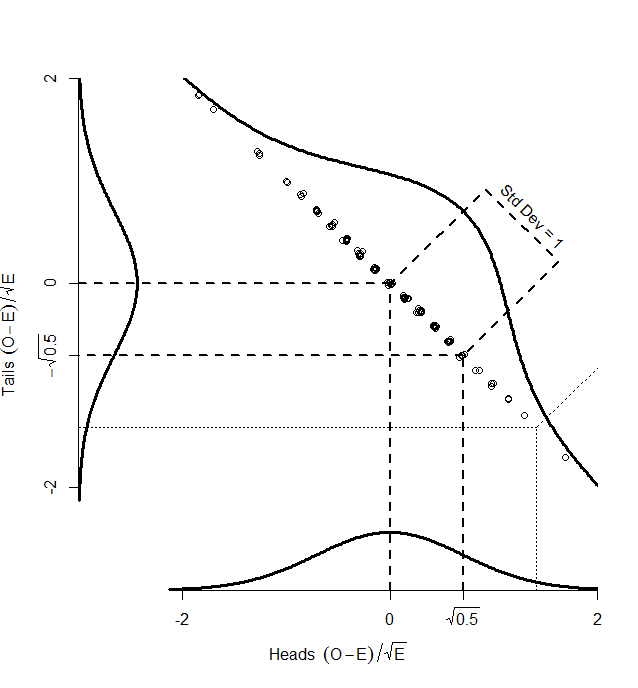
While the numbers for the heads and tails separately do not have standard deviation of 1, the dots make a diagonal pattern of a normal distribution that does have a standard deviation of 1. If you don’t believe me that this pattern has a standard deviation of 1, it’s just another application of Pythagoras’ theorem to the two standard deviations that make it up:

So, if we find the distance of each point on the graph from the centre (0,0), that distance is standard normal, and we can compare it with the numbers in the back of our text book. How do we find that distance? Pythagoras’ theorem, of course:

which we can simplify to the standard chi-squared formula:

So, we could take the square root of this, and compare it with the standard normal numbers in the back of our book. Or we could not take the square root, and compare it with a chi-square distribution with one degree of freedom (since a chi-square distribution with one degree of freedom is just the square of one standard normal).

So, the key point here is that, although we have two different observed counts, a scatterplot of them can only scatter away from the centre in one direction — the graph has been squashed flat. That is because we are dealing with proportions, so that if we gain one extra head out of our 100, we must lose a tail. And in the one direction that it can move, it is normally distributed with standard deviation of 1. So, our graph is made up of one single, standard normal distribution, and the squared distances from the centre will be chi-square distributed, with one degree of freedom.

Now, that might seem like a lot of hassle compared with the standard proportion test. But the beauty of the goodness-of-fit test is what happens when we have more than two possible categories.

Suppose we ask 99 participants to choose their favourite tinned meat, out of Corned Beef, Stewing Steak, and SPAM. We might hypothesise that none is really better than the other, so we should see an equal proportion of corned beef-, stewing steak- and SPAM-lovers in the population. But we have just 99 participants from this population, and so we can’t necessarily expect that we’ll get exactly 33 of each, since randomness is involved. Perhaps we have 32 corned beef, 32 stewing steak and 35 corned beef lovers. Is that sufficiently different from the expectation of 33 of each to disprove our original, “null”, hypothesis?

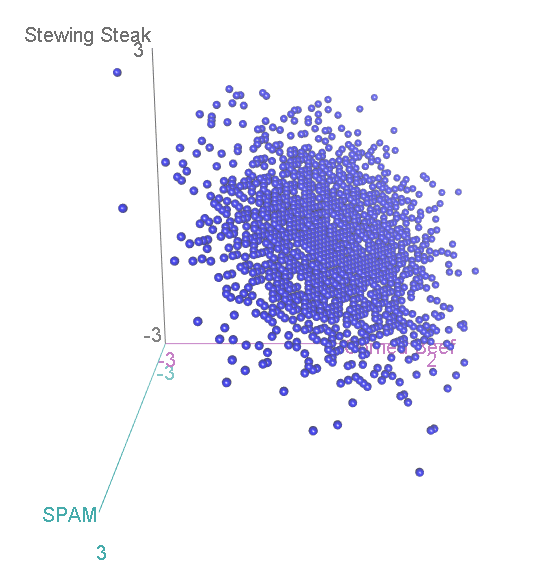
Let’s again simulate running this experiment many many times, calculate for each category, and see how the scatterplot comes out this time:

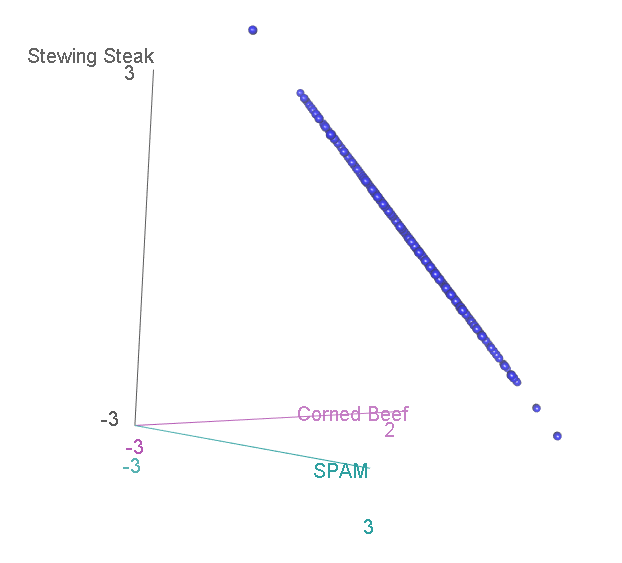
Now, we have three categories, and the scatterplot is three-dimensional. If we rotate to look side-on, we can see that, again the scatterplot is squashed flat in one dimension:

This shouldn’t be a surprise. After all, it is not possible to accumulate an extra person preferring SPAM without also losing someone who likes either Corned Beef or Stewing Steak. Now let’s look at it face-on:

This might look familiar to you? A bit, perhaps, like that scatterplot of height vs intelligence at the top:

…Actually, it is distributed in exactly the same way, again floating diagonally across a three-dimensional space. And, remember, we can look for unusual cases in this scatterplot by comparing the squared distance from the centre with two-degree-of-freedom chi-square distribution.

The proof that this is distributed in exactly the same way is quite complicated, but it leads to a very simple final solution that shows that this will hold, no matter how many categories we are dealing with. With ten categories, we have nine normal distributions lying diagonally across a ten-dimensional space, and we can compare our squared distances with nine degree of freedom chi-square distribution.

This post was really written as a way for me to wrap my head around the shape of the non-central t-distribution and how it fits into power analysis I hope it might help someone else out there, too!

My previous two posts establish the foundations for this. In the first, I showed how sample means tend to be normally distributed, and still normally distributed if we divide them by their population standard deviation; but if we divide them by their sample standard deviation they are t-distributed. In the second, I showed how the -distribution is built up as a pile of normal distributions of different spreads, but with the same mean. I’ll build on these two posts in the following.

This -distribution then forms a nice basis for testing a null hypothesis. Say we have a sample of size , with mean and standard deviation . If we want to know whether that might have come from a population with zero mean, we can calculate a -statistic as , and see if that looks like the sort of -statistic that we’d expect to get by comparing it against a -distribution with degrees of freedom.

If our -statistic is in the outer, say, 5% of what we’d expect from a distribution with zero mean, then we say it looks less likely that our null hypothesis is true, and “reject the null” (etc etc).

For example, in my the first of the posts I mention at the start, I look at the example of choosing four numbers between -48 and +48 at random. The raw numbers themselves should have a standard deviation of 28. The mean of your sample of four would, on average, come out at zero, but will miss that by a sampling standard deviation of . Dividing a given mean by this value 14 would convert it into a -score, which could then be compared against a normal distribution. Dividing by its own sample standard deviation would give us a -score which could be compared against a -distribution.

But what if our null is not actually true? Suppose we were instead choosing from the numbers -20 to +76? These numbers have the same standard deviation as before, but are shifted up by 28. Suppose we do as before: we want to see whether our mean of four numbers looks like the sort of mean we might have got from a distribution with a mean of zero. We know that the means should be roughly normally distributed, just as in the previous post, but now with a mean of 28:

So, if we divide by 14 (the true standard deviation of the mean), as we would if we were trying to get a -statistic, we just squash that normal distribution, and again get another normal distribution:

The mean of 28 also gets squashed to 1/14th its original size; of course, these don’t look -distributed, since the mean is not zero, but that is the point: half of our -statistics would be above 2, which would give us enough evidence to conclude that our sample is not consistent with one from a null hypothesis of zero mean and standard deviation of 28. So, in this example, we could conclude that we’d have 50% power.

At first look, you might think that calculating the power for a -test should be equally as simple, but let’s look at the histogram for the -scores that we would get if we divided each of our means by its own sample standard deviation:

This is lop-sided and doesn’t look anything like a -distribution. The curve that I have fitted is called the non-central -distribution and it is what we get in a situation like this. (It is a slightly rough approximation here because our raw numbers didn’t come from a normal distribution–more on this in a later post!) To understand why we get this lop-sided shape, first make sure you understand what I’m talking about in this previous post. Let’s take the code from the bottom of that post and tweak the value ncp (the “non-centrality parameter”) in this code to 2. I have chosen 2 because that is the mean of my -scores. Here’s what comes out:

When we’re dividing by a sample standard deviation that is “about right”, the mean of our means does indeed get squashed by a factor 14 and comes out around 2. But, when we get a sample standard deviation that is too large, it gets squashed even more, and the whole distribution gets squashed closer to zero, further to the left. Where the sample mean comes out too small, we don’t squash our distribution enough, so we end up spread out further to the right. When we add all these together, we get a skewed distribution. And this is the non-central -distribution. In this case, we have a -distribution with three degrees of freedom a non-centrality parameter of 2, which is the curve I fitted to the above graph.

From here, calculating power is easy. In my -test, a p-value below 0.05 corresponds to the 2.5% in each tail of our central -distribution. To keep this simple, I’ll be slightly lax and only consider the right-hand 2.5%, since I know in this example that I’ll almost certainly be to the right. In R, I can find my critical value for the -test using the following code (or I can find it in the table in the back of a statistics textbook):

> qt(.975,df=3)
[1] 3.182446


So, any -statistic above 3.18 I will declare to be statistically significant, informing me that this sample did not likely come from a distribution with zero mean. In this example, we know that the -statistics we’ll actually get will follow a non-central -distribution with non-centrality parameter of 2. All we need to do is to find out what proportion of this distribution will lie above the critical value and be declared statistically significant, which I can calculate like this:

> 1-pt(3.182446,df=3,ncp=2)
[1] 0.2885487


So, we achieve 29% power. Let’s set this up in G*Power to see if this makes some more sense of the numbers that come out of this handy piece of power-calculating software (also free, check it out!) The effect size is a Cohen’s d, which is just the distance of the true mean from the null hypothesis mean, divided by the population standard deviation: in our case that is . All the other numbers in this output should now make perfect sense to you!

And, phew, G*Power agrees with our computed power.

In my last post, I talked about how sample means tend to be normally distributed, but if we divide them by their sample standard deviation they are t-distributed. That post was really written as a supporting post for this one, and I’ll assume that you have read that post or understand these things already. Here I’ll show you a little experiment that will give you a pretty good idea of exactly how the -distribution gets its shape.

So, we’re using our sample standard deviation as an estimate of the population standard deviation. What we get then isn’t normally distributed any more because the sample standard deviation will come out different for every sample we pick:

Sometimes it will be a bit too high, which will mean we’ll be dividing our mean by a standard deviation that is too large, and our “-scores” will be “shrunk” compared with what they should be; in the top panel below I have divided by a standard deviation that is too high, so our normal distribution is squashed compared with that of a true -statistic. Sometimes our estimate of the standard deviation will be too low, and the reverse will happen: our -scores will be stretched by having been divided by too-small a standard deviation (the third panel below). The second panel is where it is about right. Since these are all divided by a single constant standard deviation, each is still normally distributed:

Since a distribution is like a “pile” of probability mass for any given score, we can combine all these possibilities by piling each pile on top of the other, and this is what I have done in the bottom graph above. The thick black line represents the top of the pile, the sum of all three of our normal distributions. The red line is a -distribution. It’s pretty close, though not exactly right–and that’s because I’m approximating by saying it will be only one of three possibilities: there are many different shades of “too high” or “too low”. But this should give you a decent idea of how the t-distribution gets its shape. The grey-shaded region is the normal distribution, which you can see is quite a different shape.

At the bottom I’ve copied my R code for generating the above plots, in case you’d like to play with it. If we increase our degrees of freedom, for example, by changing to df=10, we can see why the -distribution starts to look like a normal distribution with higher degrees of freedom: because the sample standard deviation gets closer to the right answer, and the normal distributions we are adding up start to look more and more similar:

Since we’re adding up a bunch of normal distributions that all look very similar, it’s no surprise that what we get at the end is something that looks like a normal distribution: the thick black and red lines both match the grey shaded normal distribution pretty closely.

The goal of this post is to show you that a t-distribution is just a pile of different normal distributions with different spreads. And, in fact, one way to derive the shape of the t-distribution is to add up the infinite number of different normal distributions that we could get for every different “wrong” standard deviation that we could get.

Here’s the code:


# tweak the degrees of freedom here
df = 2

# you can tweak this number if you want to explore non-central t-distributions
# the approximation I'm using falls apart a bit for very large ncp (>2), though
ncp = 0

# get standard errors that are too small, about right and too large
plotnames = c("Standard Deviation Too Small", "Standard Deviation About Right", "Standard Deviation Too Large")
SEs = sqrt(qchisq(c(1,3,5)/6,df)/df)

# plot the individual normal distributions
layout(c(1,2,3,4,4))
xs = seq(-5,5,length.out=300)
plots = sapply(SEs,function(SE)dnorm(xs,mean=ncp/SE,sd=1/SE)/3)
sapply(3:1,function(n)plot(xs,plots[,n],type="l",lwd=3,lty=4-n,ylim=c(0,max(plots)),xlab="x",ylab="p(x)",main=plotnames[n]))

# plot these normal distributions piled on top of each other
stackedplots = apply(plots,1,cumsum)
matplot(xs,t(stackedplots),type="l",lwd=3,col="black",ylim=c(0,dnorm(0)),xlab="x",ylab="p(x)",main="Sum of the Above",lty=3:1)
polygon(xs,dnorm(xs,ncp),col=rgb(0,0,0,.1),border=NA)
lines(xs,dt(xs,df,ncp),col="red",lwd=2)


Randomly pick four numbers between -48 and +48 and take their mean. There are lots of different combination that could give me a mean of zero, but to get a mean of 48, I’d have to pick four 48s in a row; a highly unlikely combination! The same goes for -48. If I ask a computer to try doing this 10,000 times, and plot a histogram of the mean I get each time, here’s how it looks:

So, you’re possibly familiar with this: the Central Limit Theorem tells us that when we take the mean of a bunch of random numbers, that mean will end up being (roughly!) normally distributed. Furthermore, it tells us that the standard deviation of this normal distribution will be where is the standard deviation of the numbers we started with and is the size of our sample. In our case, the standard deviation of the numbers -48 through 48 (if chosen with equal probability) is 28:

.

Our sample size is 4,

,

so the standard deviation of the above normal distribution should be , which looks about right for the above histogram!

Now, if we divide by this “standard error” (the standard deviation of our means), we should have numbers that are normally distributed with mean 0 and standard deviation of 1. We have -scores:

And we can compare these numbers to the numbers in our z-tables in our statistics books. We can see that, for example, getting a mean of 28 or more has only a 2.5% probability — because it has a z-score of . This also agrees with the histogram of means, where we can see there were not very many cases above 28. This is a -test, and we run a -test when we know what the true standard deviation of the population is.

What if we have a set of numbers that we are taking the mean of, but we don’t know what the population standard deviation is? Well, we could use the standard deviation of our sample as a reasonable guess at the standard deviation of the population. But since that’s just a guess, we don’t get quite the numbers we would have had before, and we end up with a slightly different shape of histogram:

The black line that I’ve fitted to this histogram is the -distribution with three degrees of freedom. (Three because degrees of freedom is ). You can see it is fatter at the edges; we saw that there was only a 2.5% chance of getting a -score of 2 or more, but there is a 7% chance of getting a -score of 2 or more in this case. So, if we don’t know what the true population standard deviation is, we can use our sample standard deviation as an estimate, but we need to compare it against a different distribution (the -distribution), which means looking at a different table in the back of your statistics book (a table referring to ““), and we call it a “-test”.

If you’re curious where the shape of this distribution comes from, my next post should give you a pretty good idea of it.

This is a question I’ve wanted to understand for quite some time. The likelihood ratio test seems to be almost a silver bullet for many of the modern maximum-likelihood approaches to statistics, but it always seemed quite mysterious to me that should have a known distribution. I’ve spent my morning today working through a few derivations for this, and it’s some dense stuff! I haven’t yet looked at the full multi-dimensional proofs, so I am no expert by any means, but I have managed to get my head around the proof of a simplified Wilks’ theorem here, and what follows is a little summary of this, partly for my own reference, and partly because I’d have found a simple overview helpful before I looked at the proper proofs, so I hope it might be helpful someone else too. Clearly, I’m no expert on this particular topic, and I’d welcome any corrections or suggested improvements.

If you don’t know what a likelihood ratio test is, or what maximum likelihood is, I refer you to Google! There is plenty of stuff out there on what they are and how they are run. What I found harder to find, however, was anything offering a simple, crude intuition of why it works. So, I thought, now that I have my head around a simple version of the derivation, it might be nice to make a quick, simple graphical summary. I gloss over a lot of technical details about different types of convergence etc here. This is just the bare bones.

To keep the maths as simple as possible, I’ll use quite a bit of loose/abusive notation; and will refer to the log likelihood, . The whole derivation is based on simple Taylor expansions around either the maximum likelihood parameter estimate or the (null hypothesis) true parameter . This seems sensible, as these two should be relatively close to each other. To keep things simple, I will discuss as if the log likelihood were quadratic — which, by our expansions, we are assuming to be true locally, anyway. (And for a normal distribution, this will not be an approximation; another beautiful thing about the normal distribution is that the log likelihood is a quadratic!). Here, then, is a plot of :

The gap between the dashed lines represents the log likelihood ratio `LR’, and we are using here a Taylor expansion to find this difference in log values (i.e. log of a ratio). Bear in mind that since we are at a maximum on the likelihood surface; this is why there is no linear term in our expansion. The key to the proof is the claim in the underbrace, that will be normally distributed around , with variance of . If we can prove that this is true, then we are done: it is clear, in this case that . Though, that does assume that the curvature in the log likelihood surface for our data is close to its expectation.

To see that it is indeed distributed like this, take a look at the derivative of the above graph:

Since we now have a straight line, then if we can show that is normally distributed, then so too should be . And, indeed, the log likelihood is found by summing the log likelihoods across all datapoints, each of which is i.i.d., so central limit theorem gives us that it is (asymptotically) normally distributed, and so too should be its derivative .

The sampling variance of the likelihood derivative for a given datapoint is known as the Fisher information, and there is a nice clean, simple proof that here on Wikipedia. Since our overall likelihood is just a sum , then

.

Finally, assuming again that is close to its expectation,

.

Here, as in a couple of places, we are treating as if it behaves like a constant , while we are treating as a random variable. This relates to Slutsky’s theorem, which I won’t go into here, but a simple way to view this is that so, as numerator and denominator above get closer to their expectations, the variance is really driven by .