Month: January 2017

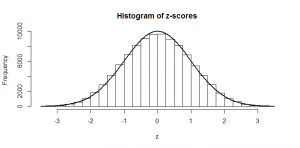
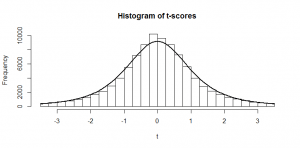
This post was really written as a way for me to wrap my head around the shape of the non-central t-distribution and how it fits into power analysis I hope it might help someone else out there, too!

My previous two posts establish the foundations for this. In the first, I showed how sample means tend to be normally distributed, and still normally distributed if we divide them by their population standard deviation; but if we divide them by their sample standard deviation they are t-distributed. In the second, I showed how the -distribution is built up as a pile of normal distributions of different spreads, but with the same mean. I’ll build on these two posts in the following.

This -distribution then forms a nice basis for testing a null hypothesis. Say we have a sample of size , with mean and standard deviation . If we want to know whether that might have come from a population with zero mean, we can calculate a -statistic as , and see if that looks like the sort of -statistic that we’d expect to get by comparing it against a -distribution with degrees of freedom.

If our -statistic is in the outer, say, 5% of what we’d expect from a distribution with zero mean, then we say it looks less likely that our null hypothesis is true, and “reject the null” (etc etc).

For example, in my the first of the posts I mention at the start, I look at the example of choosing four numbers between -48 and +48 at random. The raw numbers themselves should have a standard deviation of 28. The mean of your sample of four would, on average, come out at zero, but will miss that by a sampling standard deviation of . Dividing a given mean by this value 14 would convert it into a -score, which could then be compared against a normal distribution. Dividing by its own sample standard deviation would give us a -score which could be compared against a -distribution.

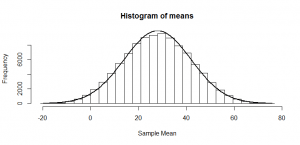
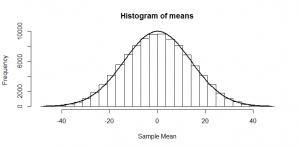
But what if our null is not actually true? Suppose we were instead choosing from the numbers -20 to +76? These numbers have the same standard deviation as before, but are shifted up by 28. Suppose we do as before: we want to see whether our mean of four numbers looks like the sort of mean we might have got from a distribution with a mean of zero. We know that the means should be roughly normally distributed, just as in the previous post, but now with a mean of 28:

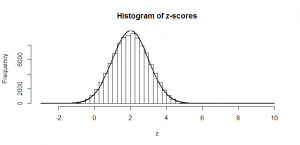
So, if we divide by 14 (the true standard deviation of the mean), as we would if we were trying to get a -statistic, we just squash that normal distribution, and again get another normal distribution:

The mean of 28 also gets squashed to 1/14th its original size; of course, these don’t look -distributed, since the mean is not zero, but that is the point: half of our -statistics would be above 2, which would give us enough evidence to conclude that our sample is not consistent with one from a null hypothesis of zero mean and standard deviation of 28. So, in this example, we could conclude that we’d have 50% power.

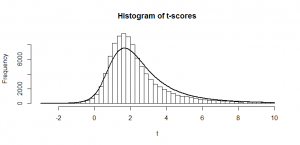
At first look, you might think that calculating the power for a -test should be equally as simple, but let’s look at the histogram for the -scores that we would get if we divided each of our means by its own sample standard deviation:

This is lop-sided and doesn’t look anything like a -distribution. The curve that I have fitted is called the non-central -distribution and it is what we get in a situation like this. (It is a slightly rough approximation here because our raw numbers didn’t come from a normal distribution–more on this in a later post!) To understand why we get this lop-sided shape, first make sure you understand what I’m talking about in this previous post. 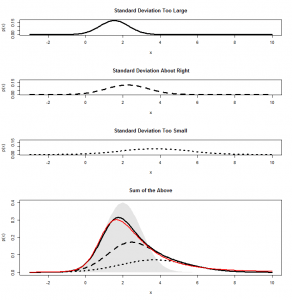Let’s take the code from the bottom of that post and tweak the value ncp (the “non-centrality parameter”) in this code to 2. I have chosen 2 because that is the mean of my -scores. Here’s what comes out:

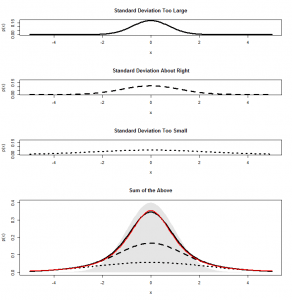
When we’re dividing by a sample standard deviation that is “about right”, the mean of our means does indeed get squashed by a factor 14 and comes out around 2. But, when we get a sample standard deviation that is too large, it gets squashed even more, and the whole distribution gets squashed closer to zero, further to the left. Where the sample mean comes out too small, we don’t squash our distribution enough, so we end up spread out further to the right. When we add all these together, we get a skewed distribution. And this is the non-central -distribution. In this case, we have a -distribution with three degrees of freedom a non-centrality parameter of 2, which is the curve I fitted to the above graph.

From here, calculating power is easy. In my -test, a p-value below 0.05 corresponds to the 2.5% in each tail of our central -distribution. To keep this simple, I’ll be slightly lax and only consider the right-hand 2.5%, since I know in this example that I’ll almost certainly be to the right. In R, I can find my critical value for the -test using the following code (or I can find it in the table in the back of a statistics textbook):

> qt(.975,df=3)
[1] 3.182446


So, any -statistic above 3.18 I will declare to be statistically significant, informing me that this sample did not likely come from a distribution with zero mean. In this example, we know that the -statistics we’ll actually get will follow a non-central -distribution with non-centrality parameter of 2. All we need to do is to find out what proportion of this distribution will lie above the critical value and be declared statistically significant, which I can calculate like this:

> 1-pt(3.182446,df=3,ncp=2)
[1] 0.2885487


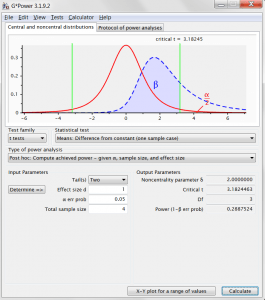
So, we achieve 29% power. Let’s set this up in G*Power to see if this makes some more sense of the numbers that come out of this handy piece of power-calculating software (also free, check it out!) The effect size is a Cohen’s d, which is just the distance of the true mean from the null hypothesis mean, divided by the population standard deviation: in our case that is . All the other numbers in this output should now make perfect sense to you!

And, phew, G*Power agrees with our computed power.

In my last post, I talked about how sample means tend to be normally distributed, but if we divide them by their sample standard deviation they are t-distributed. That post was really written as a supporting post for this one, and I’ll assume that you have read that post or understand these things already. Here I’ll show you a little experiment that will give you a pretty good idea of exactly how the -distribution gets its shape.

So, we’re using our sample standard deviation as an estimate of the population standard deviation. What we get then isn’t normally distributed any more because the sample standard deviation will come out different for every sample we pick:

Sometimes it will be a bit too high, which will mean we’ll be dividing our mean by a standard deviation that is too large, and our “-scores” will be “shrunk” compared with what they should be; in the top panel below I have divided by a standard deviation that is too high, so our normal distribution is squashed compared with that of a true -statistic. Sometimes our estimate of the standard deviation will be too low, and the reverse will happen: our -scores will be stretched by having been divided by too-small a standard deviation (the third panel below). The second panel is where it is about right. Since these are all divided by a single constant standard deviation, each is still normally distributed:

Since a distribution is like a “pile” of probability mass for any given score, we can combine all these possibilities by piling each pile on top of the other, and this is what I have done in the bottom graph above. The thick black line represents the top of the pile, the sum of all three of our normal distributions. The red line is a -distribution. It’s pretty close, though not exactly right–and that’s because I’m approximating by saying it will be only one of three possibilities: there are many different shades of “too high” or “too low”. But this should give you a decent idea of how the t-distribution gets its shape. The grey-shaded region is the normal distribution, which you can see is quite a different shape.

At the bottom I’ve copied my R code for generating the above plots, in case you’d like to play with it. If we increase our degrees of freedom, for example, by changing to df=10, we can see why the -distribution starts to look like a normal distribution with higher degrees of freedom: because the sample standard deviation gets closer to the right answer, and the normal distributions we are adding up start to look more and more similar:

Since we’re adding up a bunch of normal distributions that all look very similar, it’s no surprise that what we get at the end is something that looks like a normal distribution: the thick black and red lines both match the grey shaded normal distribution pretty closely.

The goal of this post is to show you that a t-distribution is just a pile of different normal distributions with different spreads. And, in fact, one way to derive the shape of the t-distribution is to add up the infinite number of different normal distributions that we could get for every different “wrong” standard deviation that we could get.

Here’s the code:


# tweak the degrees of freedom here
df = 2

# you can tweak this number if you want to explore non-central t-distributions
# the approximation I'm using falls apart a bit for very large ncp (>2), though
ncp = 0

# get standard errors that are too small, about right and too large
plotnames = c("Standard Deviation Too Small", "Standard Deviation About Right", "Standard Deviation Too Large")
SEs = sqrt(qchisq(c(1,3,5)/6,df)/df)

# plot the individual normal distributions
layout(c(1,2,3,4,4))
xs = seq(-5,5,length.out=300)
plots = sapply(SEs,function(SE)dnorm(xs,mean=ncp/SE,sd=1/SE)/3)
sapply(3:1,function(n)plot(xs,plots[,n],type="l",lwd=3,lty=4-n,ylim=c(0,max(plots)),xlab="x",ylab="p(x)",main=plotnames[n]))

# plot these normal distributions piled on top of each other
stackedplots = apply(plots,1,cumsum)
matplot(xs,t(stackedplots),type="l",lwd=3,col="black",ylim=c(0,dnorm(0)),xlab="x",ylab="p(x)",main="Sum of the Above",lty=3:1)
polygon(xs,dnorm(xs,ncp),col=rgb(0,0,0,.1),border=NA)
lines(xs,dt(xs,df,ncp),col="red",lwd=2)


Randomly pick four numbers between -48 and +48 and take their mean. There are lots of different combination that could give me a mean of zero, but to get a mean of 48, I’d have to pick four 48s in a row; a highly unlikely combination! The same goes for -48. If I ask a computer to try doing this 10,000 times, and plot a histogram of the mean I get each time, here’s how it looks:

So, you’re possibly familiar with this: the Central Limit Theorem tells us that when we take the mean of a bunch of random numbers, that mean will end up being (roughly!) normally distributed. Furthermore, it tells us that the standard deviation of this normal distribution will be where is the standard deviation of the numbers we started with and is the size of our sample. In our case, the standard deviation of the numbers -48 through 48 (if chosen with equal probability) is 28:

.

Our sample size is 4,

,

so the standard deviation of the above normal distribution should be , which looks about right for the above histogram!

Now, if we divide by this “standard error” (the standard deviation of our means), we should have numbers that are normally distributed with mean 0 and standard deviation of 1. We have -scores:

And we can compare these numbers to the numbers in our z-tables in our statistics books. We can see that, for example, getting a mean of 28 or more has only a 2.5% probability — because it has a z-score of . This also agrees with the histogram of means, where we can see there were not very many cases above 28. This is a -test, and we run a -test when we know what the true standard deviation of the population is.

What if we have a set of numbers that we are taking the mean of, but we don’t know what the population standard deviation is? Well, we could use the standard deviation of our sample as a reasonable guess at the standard deviation of the population. But since that’s just a guess, we don’t get quite the numbers we would have had before, and we end up with a slightly different shape of histogram:

The black line that I’ve fitted to this histogram is the -distribution with three degrees of freedom. (Three because degrees of freedom is ). You can see it is fatter at the edges; we saw that there was only a 2.5% chance of getting a -score of 2 or more, but there is a 7% chance of getting a -score of 2 or more in this case. So, if we don’t know what the true population standard deviation is, we can use our sample standard deviation as an estimate, but we need to compare it against a different distribution (the -distribution), which means looking at a different table in the back of your statistics book (a table referring to ““), and we call it a “-test”.

If you’re curious where the shape of this distribution comes from, my next post should give you a pretty good idea of it.