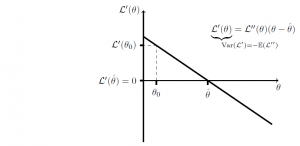This is a question I’ve wanted to understand for quite some time. The likelihood ratio test seems to be almost a silver bullet for many of the modern maximum-likelihood approaches to statistics, but it always seemed quite mysterious to me that should have a known distribution. I’ve spent my morning today working through a few derivations for this, and it’s some dense stuff! I haven’t yet looked at the full multi-dimensional proofs, so I am no expert by any means, but I have managed to get my head around the proof of a simplified Wilks’ theorem here, and what follows is a little summary of this, partly for my own reference, and partly because I’d have found a simple overview helpful before I looked at the proper proofs, so I hope it might be helpful someone else too. Clearly, I’m no expert on this particular topic, and I’d welcome any corrections or suggested improvements.
If you don’t know what a likelihood ratio test is, or what maximum likelihood is, I refer you to Google! There is plenty of stuff out there on what they are and how they are run. What I found harder to find, however, was anything offering a simple, crude intuition of why it works. So, I thought, now that I have my head around a simple version of the derivation, it might be nice to make a quick, simple graphical summary. I gloss over a lot of technical details about different types of convergence etc here. This is just the bare bones.
To keep the maths as simple as possible, I’ll use quite a bit of loose/abusive notation; and will refer to the log likelihood,
. The whole derivation is based on simple Taylor expansions around either the maximum likelihood parameter estimate
or the (null hypothesis) true parameter
. This seems sensible, as these two should be relatively close to each other. To keep things simple, I will discuss as if the log likelihood
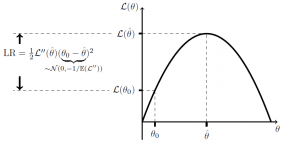
were quadratic — which, by our expansions, we are assuming to be true locally, anyway. (And for a normal distribution, this will not be an approximation; another beautiful thing about the normal distribution is that the log likelihood is a quadratic!). Here, then, is a plot of
:
The gap between the dashed lines represents the log likelihood ratio `LR’, and we are using here a Taylor expansion to find this difference in log values (i.e. log of a ratio). Bear in mind that since we are at a maximum on the likelihood surface; this is why there is no linear term in our expansion. The key to the proof is the claim in the underbrace, that
will be normally distributed around
, with variance of
. If we can prove that this is true, then we are done: it is clear, in this case that
. Though, that does assume that the curvature in the log likelihood surface for our data
is close to its expectation.
To see that it is indeed distributed like this, take a look at the derivative of the above graph:
Since we now have a straight line, then if we can show that is normally distributed, then so too should be
. And, indeed, the log likelihood is found by summing the log likelihoods across all datapoints, each of which is i.i.d., so central limit theorem gives us that it is (asymptotically) normally distributed, and so too should be its derivative
.
The sampling variance of the likelihood derivative for a given datapoint is known as the Fisher information, and there is a nice clean, simple proof that
here on Wikipedia. Since our overall likelihood is just a sum
, then
.
Finally, assuming again that is close to its expectation,
.
Here, as in a couple of places, we are treating as if it behaves like a constant
, while
we are treating as a random variable. This relates to Slutsky’s theorem, which I won’t go into here, but a simple way to view this is that
so, as numerator and denominator above get closer to their expectations, the variance is really driven by
.